Potential Energy in an Electrostatic Field

Because it may take work to move a charge in an electric field, it has an energy that depends on its position, just like a mass in the gravitational field near the surface of the Earth.

Before we go on, we should probably remind ourselves of the fact that work is the integral of force times displacement. However, since we will not use calculus as an essential ingredient in this course, we will only calculate two special cases, the work done in the E-field of a point charge (see below), and the work done in a constant E-field.

Consider a point charge Q at the origin, r = 0. It has a field of magnitude E(), which is zero only at . So a test charge q₀ would be out of the influence of the charge Q only at r = . At any other position, say , it is attracted by Q, if Q is negative, and repelled by Q, if Q is positive. If Q were positive, then the test charge q₀ would have to be pushed against the repulsion of Q to bring it from infinity to its current position, . The work that some external agent has to do to do this pushing is stored up as its potential energy .

Potential Energy of a charge q₀ in the Field due to a charge Q:

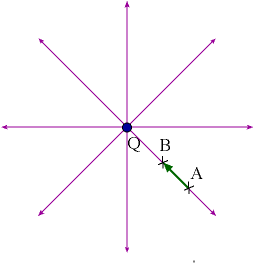
Suppose that the charge q₀ is moved from its initial position at _A to the position _B along a radial line. To figure out the work done to make this movement, we take little segments $\Delta$ on this path, and calculate

W = () · $\Delta$ = q₀· () · $\Delta$

as the total work. It is necessary to consider such little segments, because () changes with . Then we sum over all these little segments. When you actually do the integral, the result is:

This represents the work required to move the charge q₀ is moved from its initial position at _A to the position _B .

The Electrostatic Field is Conservative

A field of force is called conservative when the work done in a round trip back to the same point in this field is zero, or, alternatively, when W_BA depends only on the two end points A and B, but not on the actual path followed in going from one to the other. A look at the above equation shows that this is true for the field of a single charge. Recall that the gravitational field also has the same property.

Whenever a field has this property, one can associate a Potential Energy, U, for any charge q₀ , at each point of the field.

Then the total energy E = KE + PE is conserved:

The Zero of Potential Energy:

It really does not matter where the zero of potential energy is chosen, as potential energy is always defined up to a constant. But the above equation shows that for the electrostatic field of a single charge, it is convenient to take the zero of potential energy at infinity. With this choice,

U() = k · q₀ · Q / r

© MultiMedia Physics 2000