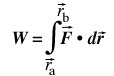
The general way to calculate the work done by a force is
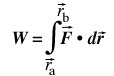
that is to say work is the integral
of the scalar product between force
and displacement. This integral is called a line-integral, because
the path taken from 
a
to b
matters. We will see in which cases the work is path-independent.
However, we will never explicitely have to make use of this integral.
Instead we will use the simpler cases below.
An immediate consequence of the scalar product above is that there is no work done by a force that is acting perpendicular to the displacement. This simple truth always holds and is at the very least something that you should take away from all of the discussions on this page.
If the motion is in one dimension, then the above formula reduces to
F dx (for 1 dimension)If the force is constant, i.e. not a function of the displacement, then we can move F out of the integral and get:
(for const. )These two special cases will be discussed in more detail in the following.
Remark:
We promised that we would not use calculus as an essential tool in this class. If the above makes it seem like we are not keeping this promise, please read the next few topics. It will then become clear that we can live without the integrals above and still solve our homework and examples. However, again, if you are heading into a technical field, you will use calculus, and the formulas above should give you a reference for future studies.
If the above is confusing to you, try this page, which gives the equivalent information needed for our course, but without using calculus.
© MultiMedia Physics, 1999