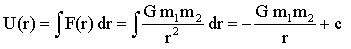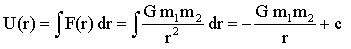Gravitational Potential Energy

We have already previously calculated the gravitational potential energy and arrived at: U = mgh. However, this expression is valid only for g = constant. If the gravitational acceleration varies, then this relation is not true any more.

Here is the solution for the more general case:

Two point masses separated by a distance r

Gravitational potential energy:

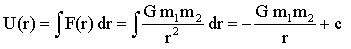
The choice of the 0 for the potential energy, that is to say the integration constant in the formula above, is such that U(r => ) = 0. The integration constant is then c = 0. We therefore get for the gravitational potential energy with this choice: \[ \rm \mathbf{U(r) = \frac{-G m_{1} m_{2}}{r}} \]
At some height h above the Earth, the gravitational potential is then:

\[ \rm \mathbf{U(h) = \frac{-G m M_{E}}{R_{E} + h}} \]

Near the surface of the Earth, h << R_E therefore \[ \rm \mathbf{(h+R_{E})^{-1} \approx \frac{1 - \frac{h}{R_{E}}}{R_{E}}} \]
then:

\[ \rm \mathbf{U(h) - U(h=0) \approx m \cdot \frac{G M_{E}}{R_{E}^{2}} \cdot h} \]

This is our old result, because we have just shown that \[ \rm \mathbf{g = \frac{G M_{E}}{R_{E}^{2}}} \]

Final remark: The gravitational potential is additive. This situation means that we can simply calculate the gravitational potential for an object by adding up all gravitational potentials due to each of its interactions with all other objects.