To
this end we introduce the angular momentum, 
.
It is defined as the cross product
of the radius and momentum vectorsLook at what we have done so far for rotational motion: We introduced angular velocity, angular acceleration, torque, and rotational kinetic energy. Basically, we have introduced equivalent concepts in angular motion for all kinematic and dynamic quantities that we had discovered in linear motion. There is only one exception, and this is the rotational equivalent of the linear momentum vector.
To
this end we introduce the angular momentum, .
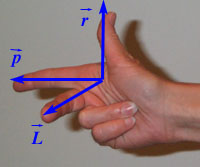
It is defined as the cross product
of the radius and momentum vectors
=
x
Why does this make sense? Lets look at the absolute values:
where r
is the distance from the axis of rotation along a line perpendicular
to the velocity vector. Since the moment of inertia, I, is the analog
of mass and the angular velocity corresponds to the linear velocity,
the angular momentum is the quantity corresponding to the momentum
(p=mv) in rotational motion. So our above definition definitely makes
sense and fits into our overall systematics.
The direction of angular momentum vector is given by the right-hand rule just as in any cross product of two vectors.
Torque can be related to the change in angular momentum. This is the rotational equivalent of Newton's Second Law. We just give the result without a derivation:
Calculus version:
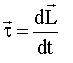
Non-calculus version:
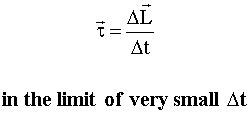
© MultiMedia Physics, 1999