We defined kinetic energy as:
Because p = m v, we get:
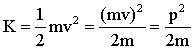
Therefore the kinetic energy can also be written as the square of the absolute value of the momentum, divided by twice the mass.
An external force is required to change the momentum. In fact, the time derivative of the momentum is equal to the external force:
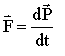
This statement is equivalent to Newton's Second Law. It is more general, however, in that this relation even holds for masses that can vary with time, whereas the conventional F = m a does not.
For your convenience, here is also the equivalent formulation of the last equation without the use of calculus:
The rate of change of the momentum equals the external force:
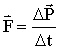
© MultiMedia Physics, 1999