In translational motion, a force,
![]() , is
required to produce a change in translational motion, i.e. an
acceleration:
, is
required to produce a change in translational motion, i.e. an
acceleration:
where m is the mass and ![]() is the linear acceleration. (Newton's
Second Law).
is the linear acceleration. (Newton's
Second Law).
In complete analogy, in rotational motion a torque, ![]() ,
is required to produce a change in rotational motion,
,
is required to produce a change in rotational motion,
where I is the moment of inertia (we will explain later in much
more detail what this is), and ![]() is the angular acceleration. Please note that the torque is a vector
quantity, as is the angular acceleration. They point in the same
direction.
is the angular acceleration. Please note that the torque is a vector
quantity, as is the angular acceleration. They point in the same
direction.
A torque is the cross product
between force and moment arm - it is produced by exerting a force F
with a moment arm r>![]() :
:
 Here
r
Here
r![]() = r sin
= r sin![]() sin
sin![]() that is perpendicular to the force vector
that is perpendicular to the force vector ![]() .
The torque
.
The torque ![]() points in a direction
points in a direction ![]()
![]() and to the vector
and to the vector ![]() .
.
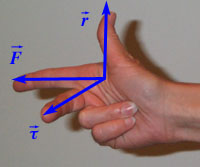
You can again use the right-hand-rule (see figure on the right) of
the cross product to determine which way the torque is pointing. So
if ![]() and
and
![]() are in
the plane as shown, and the middle finger points out of the screen,
that means that the torque is counterclockwise. A middle finger
pointing into the screen would correspond to a clockwise torque.
are in
the plane as shown, and the middle finger points out of the screen,
that means that the torque is counterclockwise. A middle finger
pointing into the screen would correspond to a clockwise torque.
The magnitude of the torque from the above equation is:
© MultiMedia Physics, 1999