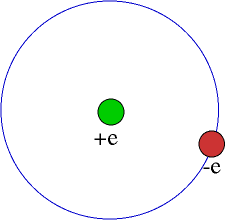
 According
to the Bohr model, the hydrogen atom consists of a proton of charge
+e and an electron in circular orbit around it with charge -e. The
electron can exist only in orbits for which the angular momentum is
an integral multiple of (h/2
According
to the Bohr model, the hydrogen atom consists of a proton of charge
+e and an electron in circular orbit around it with charge -e. The
electron can exist only in orbits for which the angular momentum is
an integral multiple of (h/2 According
to the Bohr model, the hydrogen atom consists of a proton of charge
+e and an electron in circular orbit around it with charge -e. The
electron can exist only in orbits for which the angular momentum is
an integral multiple of (h/2
According
to the Bohr model, the hydrogen atom consists of a proton of charge
+e and an electron in circular orbit around it with charge -e. The
electron can exist only in orbits for which the angular momentum is
an integral multiple of (h/2![]() where h is
Planck's constant. The angular
momentum of a mass m in a circular orbit with radius r is
where h is
Planck's constant. The angular
momentum of a mass m in a circular orbit with radius r is
so that Bohr's condition requires
where rn is the orbit radius corresponding to the integer n. If we now solve for v and then square v, we get
From Newtonian mechanics entering the derivation of the Kepler Laws (this analogy works, because the gravitational and electrostatic forces have the same dependence on r) we know that the centripetal force is provided by the Coulomb attraction between the electron and the nucleus (charge Ze) and is given by
so we get

From this result, we can obtain the radius of the nth orbit by substituting the classical expression for v2 with Z =1 into the Bohr quantum model
where k = 9.0·109 N·m2/C2.
We can rewrite this formula as rn = n2ao where
which is called the Bohr radius.
In the drawing to the right, the first four orbits are drawn to scale. The orbit corresponding to n = 1 has the radius r1 = ao. The electron may not reside in any orbit between these orbits. The radii are quantized meaning that when the electron is in one of these orbits, it does not radiate away energy by gradually slowing down.
© MultiMedia Physics 2000