Newton's Law of Gravitation

So far, we have always treated the gravitational acceleration as a constant. This approach is approximately correct near the surface of the Earth, but not in general. The general gravitational force law explains the gravitational acceleration that falling objects near the surface of Earth experience and at the same time explains how planets and stars move in their orbits. This discovery goes back to Newton, who also gave us the famous three force laws, as well.

Universal Law of Gravitation (Isaac Newton):

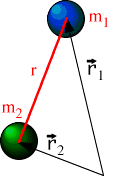
Any two objects attract each other gravitationally with equal and opposite forces pointing towards each other. The magnitude of this force is:

\[ \rm \mathbf{F(r) = \frac{G m_{1}m_{2}}{r^{2}}} \]

Here m₁ and m₂are the masses of the two objects, and r is the distance between the two object,

r = |

₁-

₂|.

G is called the universal gravitational constant,

G = 6.67 $\cdot$ 10^-11 N$\cdot$ m²/kg²

Remark: For points located outside of homogeneous spheres, gravity acts in the same way as between point particles located at the center-of-mass coordinates (centers of the spheres).