Gravity near the Earth's Surface

What is the gravitational acceleration of a mass m located at some distance r with respect to the center of the Earth?

Because F = ma, we have for the gravitational acceleration, g(r)

\[ \rm \mathbf{m g(r) = F = \frac{G m M_{E}}{r^{2}}} \] \[ \rm \mathbf{ g(r) = \frac{G M_{E}}{r^{2}}} \]

where M_E is the mass of the Earth.

If the mass m is now located some distance h (h <E) above the surface of the Earth, then we have:

\[ \rm \mathbf{g(r) = \frac{G M_{E}}{(h+R_{E})^{2}} \approx \frac{G M_{E}}{R_{E}^{2}} = constant} \]

where we neglect h in the last step because h is much smaller than R_E.

Putting in the numbers:

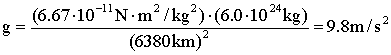
This result means that the (constant) gravitational acceleration we have been working with in previous chapters is still a valid approximation and represents a special case in the universal law of gravitation.

Although the mass of an object is the same no matter where it goes in the universe, its weight is not. Because of the universal law of gravitation, g on some other planet depends on the inverse of the square of the radius and the mass of the planet. You can see your weight on another planet on the Exploratorium website.

Regarding the direction of the force of gravity: In Newton's law of gravity we say that the force of gravity works in radial direction. Since we are located on the surface of a sphere, all objects fall straight "down", i.e. in radial direction. This ensures that levels like the one shown here work equally well here in the U.S. as they do in, say, Australia.