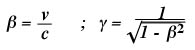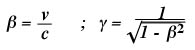Beta and Gamma

As the calculation of time dilation has shown, the factor $\gamma$ plays a prominent role. It thus pays to take a look at the behavior of $\gamma$ as a function of the speed v, or equivalently as a function of the ratio $\beta$ of the speed relative to the speed of light,

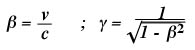
The speed of light, c, is given by:

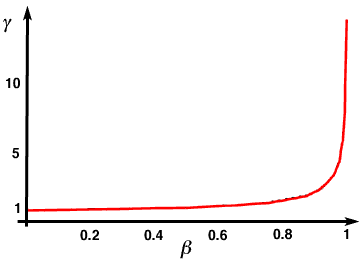
It is very instructive to plot $\gamma$as a function of $\beta$. This is done in the plot below. For speeds that are small compared to the speed of light, $\beta$ is very small, approximately equal to 0. In that case, $\gamma$ is very close to the value 1. However, as $\beta$ approaches 1, $\gamma$ diverges, that is to say grows larger and larger towards infinity.

There is also a useful approximation that is valid for low speeds. In that case v is small compared to c and therefore $\beta$ is small compared to 1, and we can approximate $\gamma$ as:

$\gamma$ 1 + 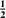$\beta$²
(for $\beta$ small compared to 1)

© MultiMedia Physics 2000