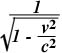Time Dilation

One of the most amazing consequences of the theory of relativity is that time is not constant and independent of the reference frame any more. Instead, time in a moving reference frame is dilated (= made longer):

$\Delta$t = $\gamma$ · $\Delta$t_o =

· $\Delta$t_o

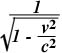This means that your time flows at a rate that depends on the speed with which you are moving. This result is truly revolutionary. It sounds like science fiction. But it has experimentally verifiable consequences - as we will see in the following examples.

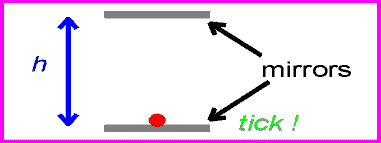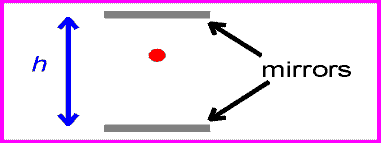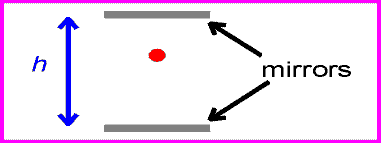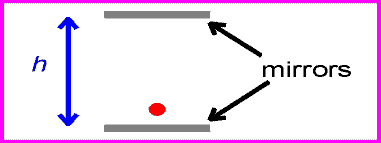
How can we derive or even just motivate this result? Let us construct a clock that keeps time by bouncing a light beam of a mirror. If we know the distance, h, between mirror and clock, then the time that it takes for the beam to go up is:

$\Delta$t_o =	h

	c

where the subscript "o" refers to the fact that the observer of this time interval is not moving. (It takes, of course, the same time for the way down, too.)

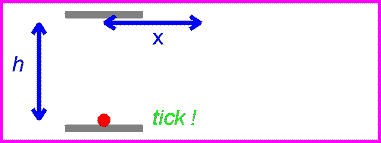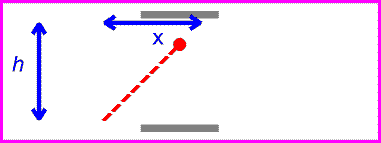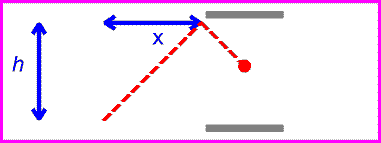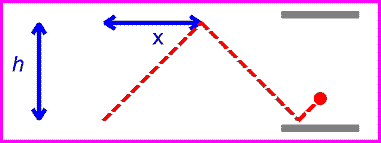
Now let's have the observer have a speed of v. You can see from the animation on the right that in this case the observer sees the light beam have a path length of

L = (h² + x²)^1/2

which is simply a consequence of Pythagorus' Theorem.

Now we have for the right-left motion

x = $\Delta$t · v

and for the bottom-top motion we can use the above equation relating h and $\Delta$t_o.,

h = $\Delta$t_o · c

($\Delta$t refers now to the time interval in the moving system.) During the same time $\Delta$t the light beam moves a path length

L = $\Delta$t · c

This is where the second postulate enters in its essential way: the light beam can only travel with c, the constant velocity of light, independent of the speed of the observer!

Insert this into the result of Pythagorus Theorem above and get:

$\Delta$t · c = ([$\Delta$t_o · c]² + [$\Delta$t · v]²)^1/2

Solve this for $\Delta$t and get:

$\Delta$t =

· $\Delta$t_o:= $\gamma$ · $\Delta$t_o

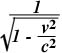In order to keep the velocity of light independent of the speed of the observer, we had to admit that the observer's time is dependent on his/her speed. An amazingly bold step, don't you think?

Notation:

Sometimes you will see the time in the rest frame of an object referred to as proper time. The proper time interval here is $\Delta$t_o.