Polar Coordinates

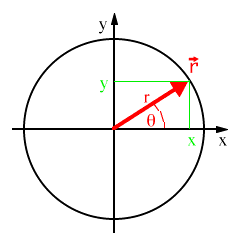
To describe the two-dimensional position vector, , in circular motion it is not convenient to work in cartesian (x and y) coordinates.

Rather: Introduce Polar Coordinates, r and q, where r is the length of the vector , and $\theta$ is its angle to the positive x-axis.

Transformation from cartesian to polar:

r = (x² + y²)^1/2 \[ \rm \mathbf{\theta = tan^{-1}\frac{y}{x}} \]

Transformation from polar to cartesian:

x = r cos$\theta$
y = r sin$\theta$

Big advantage: r does not change during circular motion. This leads to motion that can be described using the angle $\theta$ only as a variable.

Even though the motion is in a two-dimensional plane, circular motion can be described as one-dimensional.