
Example: Inclined Plane
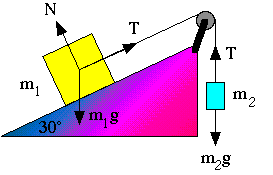
Two masses are connected by a massless string running over a
frictionless pulley as shown. One mass (m1=4.0 kg) slides
on a frictionless inclined plane inclined at 30°. The other mass
(m2=3.0 kg) is freely suspended.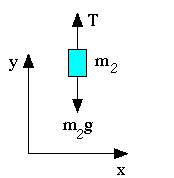
Question:
What is the acceleration of the system?
Answer:
- Let's start with m2:
- Here is its free body diagram:
- There are no forces in the x direction so:
SFx =
0
- There are forces in the y direction:
SFy = T -
m2 g = m2a2
- Now work on m1:
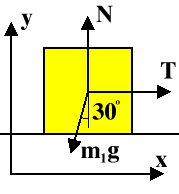
- Consider the x direction to be along the slope of the
plane,
S Fx = T -
m1 g sinq = m1
a
- Then the y direction will be perpendicular to the plane:
S Fy = N -
m1 g cosq =
0
The y equation just states that the block stays on the surface
of the plane:
N = m1g cosq
(For more help with the trigonometry of
this part, click here.)
- Now let's look at a1 and a2.
- When a2 is negative, a1 is positive:
a1 = -a2
- Let's define the acceleration a in terms of a1
and a2:
a1 = a; a2 = -a
- Rewrite our equations as
|
T - m2g
|
= -m2a
|
|
T - m1g sinq
|
= m1a
|
- Solve these two equations for T and equate the two
expressions:
-m2 a + m2 g = m1 a +
m1 g sinq
- so we can solve for a:
a = (m2g - m1g sinq)/(m1
+ m2)
- Putting in the numbers yields:
a = 1.4 m/s2
- This whole example may strike you as pretty complicated. And
it is. But the good news is that this is about as complicated an
example or a homework problem as you will come across in the
entire course. It is thus in a sense typical for the mastery of
the skills that are needed for this level of introductory physics:
isolatinf relavant variables, drawing free-body diagrams,
combining equations, some algebra and trig.
© MultiMedia Physics, 1999




