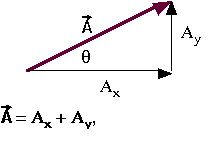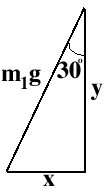In order to solve this problem, we have to find the components of the force "m₁g".

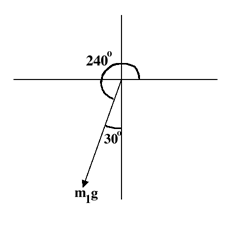
• First, we have to figure out in what direction this force is oriented. In the initial setup, m₁g was 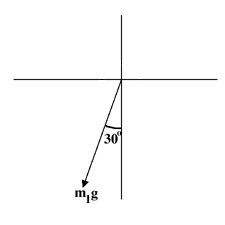pointing straight down along the y axis, the direction that gravity pulls. In order to simplify the calculation of T and N, we rotated our perspective 30 degrees clockwise, so that T was aligned with the new x axis, and N was aligned with the new y axis. This means that m₁g will be oriented 30 degrees in the clockwise direction from the y axis.

• Normally, when determing the components of a vector, we've used the method:

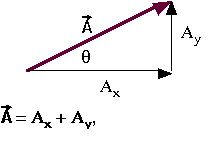
A_x = A cos q

A_y = A sin q

When we use this method, we measure the angle, q, starting at the x axis and going in the counter-clockwise direction. We could still use this method to solve the problem we're dealing with now, by determining the angle of the m₁g vector relative to the x axis:

• Another way to determine the components would be to use some simple trigonometry. What we have is a right triangle whose hypotenuse is m₁g, and whose legs are the x and y components of m₁g:

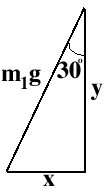
Just as we did above, we can determine the x and y components using the rules for Sine and Cosine in a right triangle:

Therefore:

Remember, however, that these are just the magnitudes. We have to consider the sense of the problem in order to determine their signs. Since m₁g points in the negative x and negative y direction, the x and y components must also be negative. Thus, our final result is: