Electric Field near a Metal Surface

Consider a metallic surface having a surface charge density $\sigma$(i.e. charge per unit area),

$\sigma$= q / A

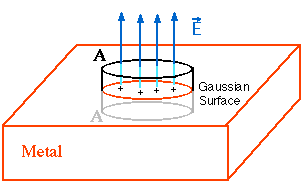
placed in a medium of permittivity $\epsilon$. Consider now a Gaussian surface of the shape of a right cylinder with its sides perpendicular to the metallic surface. One end face of area A of the Gaussian surface (circle, shown in gray) is inside the metal, while the other end face of area A (circle,shown in black) is in the medium. The red circle in the drawing shows the intersection of the Gaussian surface with the surface of the metal.

The charges are uniformly distributed over the surface of the metal. Here we have only drawn a few inside the Gaussian cylinder, but they are located everywhere on the metal surface.

Now let us apply Gauss' law. Since the lines of force are normal to a conductor, they do not intersect the side surface of the cylinder, thus the flux through these surfaces is zero. The base that is inside the metal also has zero flux, since the field here is zero. So we get

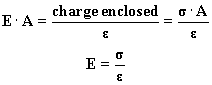
In other words:

The electric field on the surface of the metal is the surface charge density of the metal, divided by the permittivity of the medium.