Gauss' Law

Gauss' Law is an another way of expressing the fundamental law of electrostatics - Coulomb's law. It gives us an alternative viewpoint, which is useful in many physical situations of interest. It is generally stated in terms of a concept called flux of electric field.

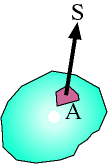
The word flux means flow. When we talk about the flux of electric field across a surface, we mean how many lines of force of the field pass through the surface, perpendicularly to that surface. You may recall from our earlier discussion that a surface area is actually a vector: its magnitude is the area, and direction is along the outward drawn normal to the surface.

Definition:

The electric flux, $\Phi$_E, through a surface is defined as the scalar product between the electric field and the surface area vector, , $\Phi$_E=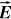 $\cdot$ = E$\cdot$S cos$\theta$,
where $\theta$ is the angle between and .

The SI unit of Flux is N$\cdot$m²/ C, or V$\cdot$m

Gauss' Law now provides a connection between the electric flux through the surface and the charge contianed inside the surface.

Gauss' Law:

Non-calculus version:
The total flux of electric field over any closed surface is equal to the net free charge q enclosed inside it, divided by the permittivity of the medium inside the surface. $\sum$E cos$\theta \cdot$S = q /$\epsilon$
where the sum is over the entire closed surface.

Calculus version:

The total electric flux integrated over any closed surface is equal to the net free charge q enclosed inside it, divided by the permittivity of the medium inside the surface. d$\Phi$_E=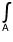 d = q /$\epsilon$

Gauss' law is mainly applied to situations with spherical or cylindrical symmetry, bacause these are the only situations in which we can deal with the resulting mathematical complexity. For some qualitative considerations, however, Gauss' Law will turn out to be extremely helpful.