Equations of Motion

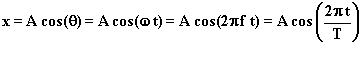
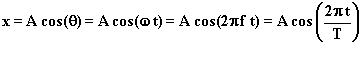
The equation of motion of an object gives its position as a function of time. The equation of motion of an object undergoing SHM can be thought of as the projection of an object undergoing circular motion with constant angular velocity $\omega$. We have convinced ourselves of this functional shape).

The period, T, and frequency, f, of a mass, m, connected to a spring with constant k undergoing SHM are given by

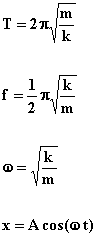
This equation of motion assumes that at t = 0 the object in simple harmonic motion starts with zero velocity and maximum displacement. Later, we will generalize this equation of motion to a general sinusoidal function with arbitrary phase shift, but the expressions for period and frequency will still hold.

Here is a great way to see how oscillatory and circular motion are connected. You can see that you may think of oscillation as a projection of circular motion onto one of the axes.

The red ball is undergoing circular motion with constant angular velocity w. Its y-component, the red line, undergoes SHM with the same angular frequency.