 |
 |
|
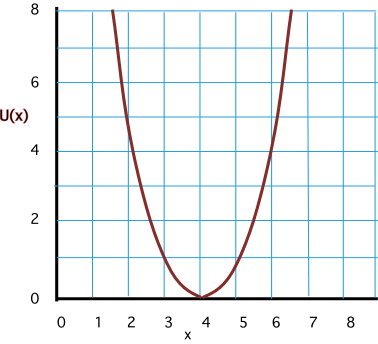
Potential energy of a spring at x = 4
|
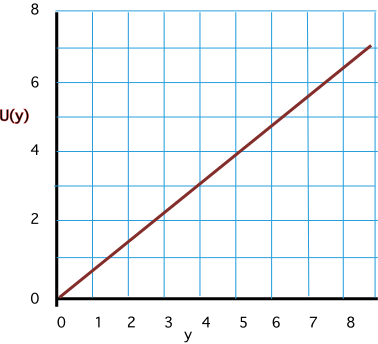
Potential energy as a function of height y
|
Potential energy is a function of position only. It can depend on x like a spring:
U(x) = 1/2 kx2
or on y the height above the ground:
U(y) = mgy
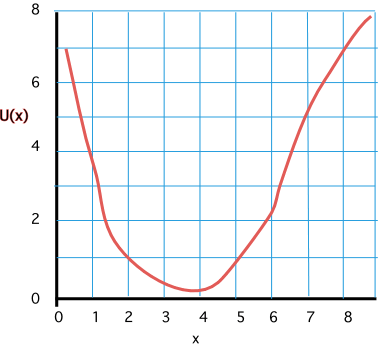
or it can have an arbitrary dependence as in the third of the three potential energies shown below. Note that the force on the object is the negative of the slope of the potential energy curve.
For a spring:
F(x) = -dU/dx = -kx (the spring force)
or for gravity near the surface of the earth:
F(y) = -mg (gravity)
 |
 |
|
Potential energy of a spring at x = 4
|
Potential energy as a function of height y
|
 |
|
An arbitrarily drawn potential energy graph
|
For systems without friction, Etotal, the total energy is conserved:
U(x) + K(x) = Etotal = constant
This allows an easy visualization of the motion (including its end points) without using forces at all. The kinetic energy K is just given by:
K(x) = 1/2 mv2 = Etotal - U(x)