Work Done by a Constant Force
The work done by a constant force in moving an object is
equal to the product of the magnitudes of the displacement and the component
of the force parallel to the displacement. Work is a scalar quantity.
When the force and displacement are in the same direction,
the work, W, is given by
W = F $\cdot$ d
If the force and the displacement are not parallel, work
is given by
W =  $\bullet$
$\bullet$ 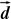 = |
= | |
$\cdot$ |
|
$\cdot$ |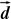 | $\cdot$ cos$\theta$ = F$\cdot$d = (F$\cdot$cos$\theta$)
$\cdot$ d = F $\cdot$ d $\cdot$ cos$\theta$
| $\cdot$ cos$\theta$ = F$\cdot$d = (F$\cdot$cos$\theta$)
$\cdot$ d = F $\cdot$ d $\cdot$ cos$\theta$
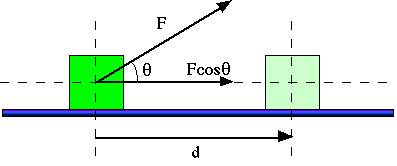
Here the bullet ($\bullet$) is the symbol for the scalar
product, and F|| is the component of  parallel to
parallel to 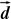 . Clearly,
if the two are in the same direction, then $\theta$=
0, cos$\theta$ = 1, and W = F $\cdot$ d, as in the
special case mentioned at the top.
. Clearly,
if the two are in the same direction, then $\theta$=
0, cos$\theta$ = 1, and W = F $\cdot$ d, as in the
special case mentioned at the top.


![]() parallel to
parallel to ![]() . Clearly,
if the two are in the same direction, then
. Clearly,
if the two are in the same direction, then