Relative Velocity - Stream Crossing Problem

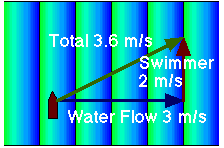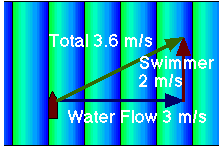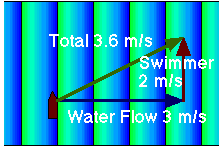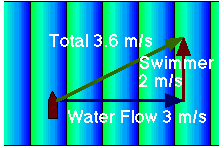
The most common form of vector addition problem is the adding of velocities. For example, we will now deal with a swimmer crossing a flowing stream. In this case the vector equation looks deceptively simple, like this:

where is the velocity of the swimmer and is the velocity of the water, as shown in this animation.

Question:

A stream flows at 3 m/s and is 100 m wide. You want to swim across at 2 m/s. Do you ever make it? How long does it take, and where do you end up? (Take the x-axis to be in the stream direction and the y-axis to be across.) What is ? (work in x- and y-components)

Answer:

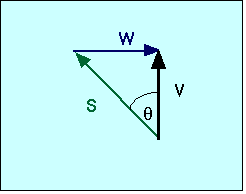
The components of the vectors and are: s_y = 2 m/s; s_x= 0; w_y = 0; w_x= 3 m/s
For their sums we then get:
v_y= s_y+ w_y = 2 m/s + 0 m/s = 2 m/s
and
v_x = s_x+ w_x = 0 m/s + 3 m/s = 3 m/s
the magnitude and direction of v are given by
v = (v_x + v_y)^1/2= (2²+3²)^1/2 = 3.6 m/s
tan ^-1(2/3) = 33.6°

Question:

How much time does it take the swimmer to cross a 100 m wide stream?

Answer:

We can use one of our kinematic equations from the previous chapter: y = y₀ + v_y0 $\cdot$ t
(no acceleration) with y₀= 0, v_y0 = 2 m/s, y = 100 m
\[ \rm t = \frac{y-y_{0}}{v_{y0}} $\Rightarrow$ t = 50s \]
This is the same time it would have taken without current! But this is a special case, because the swimmer swims exactly perpendicular to the current.

Question:

How far downstream does the swimmer end up on the other shore?

Answer:

Again we resort to our kinematic equation, this time calling the variable x instead of y: x = x₀ + v_x0t
with x₀ = 0, v_x0 = 3 m/s, t = 50 s
=> x = (3 m/s)$\cdot$(50 s) = 150 m

Question:

What is the total distance swum?

Answer:

The total distance we obtain from Pythagoras' Theorem as: d = (x² + y²)^1/2 = (100² + 150²)^1/2 m = 180.3 m

Question:

What was the swimmer's speed as observed by somebody standing on the shore of the river?

Answer:

We can get the speed in two different ways:

Since we know the individual velocity components of , we can calculate the length of that vector to get the speed: v = (2² + 3²)^1/2 m/s = 3.61 m/s

We also already calculated the total distance swum and the time it took. Take the ration of these two, and hopefully you will get the same result: \[ \rm v = \frac{d}{t} = \frac{180.3 m}{50 s} = 3.61 m/s \]

Question:

Now the hard problem. How do I swim to get directly across? In mathematical terms, how can I have V_x = 0?

Answer:

It is impossible because || > ||. Even if I swim directly upstream, I still have an x-component.

Make a new problem with a boat that can go 5 m/s.

Question:

Which angle does this boat have to select to get directly across the stream?

Answer:

must be at an angle such that v_x = 0. But v_x = w - s sin$\theta$; so the angle is given by

\[ \rm sin$\theta$ = \frac{w}{s} = \frac{3}{5} = 0.6 \]
=> $\theta$ = 37º

Question:

How long does it take?

Answer:

The stream is 100 m wide. So all we need to do is to calculate the y-component of our velocity vector, and divide 100 m by it: v_y = s cos$\theta$ = 5 m/s cos 37º = 4 m/s
\[ \rm t = \frac{y}{v_{y}} = \frac{100 m}{4 m/s} = 25 s \]

Note that if I had headed straight across, it would have taken 100/5 = 20 s, but I would have ended up 60 m downstream.