Diffraction Grating

Previously we discussed the superposition of two waves from a double slit. Suppose instead that we have thousands of slits instead of two. This arrangement is called a diffraction grating. In a diffraction grating the slits are replaced by fine lines inscribed on a piece of glass or plastic.

In a diffraction grating, one assumes that each slit emits light. This light can interfere with light from a neighboring slit or with light from several slits away. When illuminated by a monochromatic light source, a diffraction grating with many closely spaced slits produces a series of extremely sharp, intense maxima.

If we illuminate a diffraction grating with light of wavelength $\lambda$v and look at the resulting interference maxima on a screen, the angles of the maxima are given by

\[ \rm \mathbf{sin \theta_{m} = \frac{m \lambda}{d}; m = 0, 1, 2, 3, ...} \]

The maximum corresponding to m = 1 is called first order, m = 2 is called second order and so on. For gratings with very large number of lines per unit length, there is a maximum order visible

m_max is the largest integer less than d/$\lambda$.

Gratings are often labeled in term of lines per inch. To obtain d from the number of lines per inch, L

d = (0.0254 m) / L.

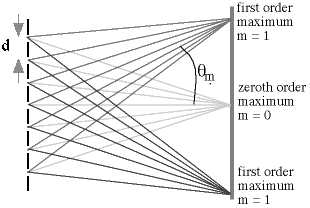
The screen is so far away that all of the light gray lines have the same path length and join to make the m = 0 maximum. Each of the rays in the darker gray bundles is one wavelength longer or shorter than its neighbor, and you get the m = 1 or first order maximum.