Concave Mirror Image

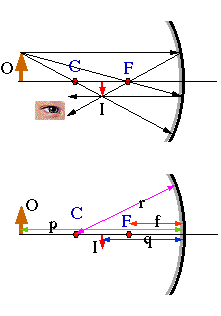
It is always possible to construct the image with the ray tracing techniques and the three special rays just discussed (see upper figure):

All light rays emitted from the tip of the arrow and reflected by the mirror are intersecting in one location. To the observing eye this looks as if the light rays emerge from there, and thus this is the location at which the image is formed. Please note that we put the bottom of the arrow exactly on the axis. This ensures that the bottom of the image is also on the axis.

We define the object distance, p, as the distance (along the axis) of the object to the mirror. The image distance, q, is the distance between the image formed and the mirror (see lower figure).

The mirror equation relates these to the focal length, f:

The magnification, M, is the ratio of the size of the image to the size of the object. One can show (by using simple geometry) that the magnification is also the negative of the ratio of image distance and object distance:

• The sign of the image distance tells us of the image is real (= in front of the mirror) or virtual (= behind the mirror):
  • q < 0 => virtual image
  • q > 0 => real image
• The sign of the magnification tells us if the image is upright or inverted:
  • m > 0 => upright image
  • m < 0 => inverted image
• The absolute value of the magnification tells us something about the size of the image formed:
  • |m| > 1 => enlarged image
  • |m| < 1 => reduced image

  © MultiMedia Physics 2000