Equipotentials

You may ask yourself now just what are all these quantities like electrostatic potential and potential energy good for? Here is a first glimpse into the power of these considerations: equipotential lines.

Consider a set of charges producing a certain electrostatic field in a certain region. Alternatively, we could think of the potential at any point due to these charges.

Definition:

All points having the same value of potential form a three dimensional surface in space, called an equipotential surface.

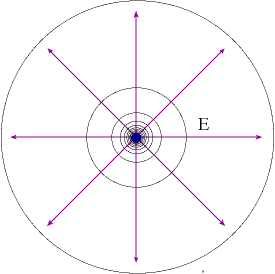
Usually the equipotential surfaces are plotted spaced in equal steps. That is done to ensure that the potential difference between any two neighboring equipotentials is the same. Equipotentials for a point charge, for example, are plotted to the left.

Consider a single point charge Q at origin. The potential due to it is

V() = k Q / r

Imagine a sphere of radius R about this charge. Since all points on this sphere have r = R, they all have the same value of the potential, k Q / R - so this sphere is an equipotential surface. It is clear that any other concentric sphere is also another equipotential.

When we make a plot, we usually display a two-dimensional section through space. In two dimensions, equipotential surfaces become equipotential lines, the lines where the equipotential surfaces intersect with the plot area (such as the circles shown in the plot).

Just as the force of gravity is a constant anywhere on a particular contour, the electric field has no component along an equipotential. Hence, when a charge is taken along an equipotential at constant speed, no work is done on it. Another way to express the same idea is to say that the work done in moving the test charge q₀ from the point 1 to the point 2 without any acceleration is q₀(V₂-V₁) = 0, since V₁ = V₂ on the equipotential.

Finally, please note that we have also drawn the electric field lines in this plot (radial purple arrows). You can see that the intersection of each field line with each equipotential line happens at a 90° angle. This is no coincidence and indeed a general property:

Equipotential lines and field lines are always perpendicular to each other.

 © MultiMedia Physics 2000