Coming back to speed, if the particle is at x(t) at time t and at x(t + D t) (which we also call x + Dx) at time t + Dt , then instantaneous speed is
1.1 Limit
Come to think of it, 'instantaneous speed' seems like a contradiction of terms. Speed is always some distance over the time required to cover that distance. How could we talk about its value at an instant -- a moment of time, which has no duration at all !
It is this contradiction that made Newton think of the concept of limit :
consider a small interval of time, Dt , and think of making it smaller and smaller -- smaller than any small number you can think of, but not (exactly equal to) zero . This is written as lim Dt ->0 , and read as "limit Dt tending to zero".
Such an idealized interval is also called an 'infinitesimal' change of t: dt.
Now suppose y is a function of the independent variable t, y(t). As t -> a particular value, say t0 , that is we consider successive values of t closer and closer and closer to t0, we look at the corresponding values of y(t). If these show a definite trend, coming closer and closer to a particular value, say l, then we say that " as t -> t0, y(t) -> its limiting value .
Example: Consider y to be first sin, and then tan, and t0 to be p/2 (= 90°). As t -> p/2
t --> p/2-
t --> p/2+ t sin t tan t
t sin t tan t 88o 0.9993 39 28.6362
92o 0.9993 39 -28.6362 89o 0.9998 48 57.2800
91o 0.9998 48 -57.2800 89o30' 0.9999 62 114.589
90o30' 0.9999 62 -114.589 89o50' 0.9999 96 343.774
90o10' 0.9999 96 -343.774 Studying the above data , you can see that as t -> 900(or p/2), either in the sequence of values < 900, shown in the left column, or in the sequence of values > 900, shown in the right column, sin t -> 1. The fact that sin(p/2) is also equal to 1 is a coincidence, and has nothing to do with the limit.
Studying the data for the tan, however, you'll notice that as t -> 900 - ,as shown in the left column, tan t becomes bigger and bigger without a bound, and thus does not approach any definite value. Again, as t -> 900+, as shown in the right column, tan t becomes more and more negative without a bound, and again does not approach a definite value. So tan t does not have a limit as t -> p/2 .
It is possible to find other examples where the left side comes to definite limit, and the right side comes to another definite limit. But the function will not have a definite limit unless the left-hand and the right-hand limits are equal.
1. 2 Differentiation
Coming back to speed, if the particle is at x(t) at time t and at x(t + D t) (which we also call x + Dx) at time t + Dt , then instantaneous speed is
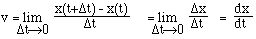
This is called "differentiation of x with respect to t", or "derivative of x with respect to t" , and is written v = dx/dt . Do not think of it as dx over dt, but rather as " of x", or
as operating on x(t).
Then
Therefore the average velocity is:
and thus the instantaneous velocity is:
1.3 Derivative and slope of the tangent
Plot the graph of y(t) vs t. Clearly,
is the
slope of the chord PQ to the graph of y(t) vs t, between t and t+Dt . As Dt is made smaller and smaller, the chord becomes smaller and smaller, with the point Q moving towards P along the curve of y(t). As Dt -> 0, Q practically coincides with P, and the chord becomes the tangent to the curve at P.
Thus, dy/dt means the slope of the tangent to the graph of y(t) vs t at the point t.
1.3 Maximum or Minimum of y(t)
If dy/dt is > 0, the tangent has positive slope, the graph is increasing (see points 1 or 6 in the diagram). If dy/dt is < 0, the tangent has negative slope(points 3 or 4), the graph is decreasing. At the point of a maximum or of a minimum, dy/dt = 0 (points 2 or 5).
Near but to the left of a maximum, the tangent would always have a positive slope (but gradually becoming less
and less positive). Then it is horizontal (slope = 0) at the maximum. Finally , after crossing the maximum, it has negative slope (and gradually becoming more and more negative). Thus the rate of change of the slope dy/dt, d2y/dt2 ( symbol for derivative of dy/dt with respect to t) is negative at maximum.
Near a minimum, the tangent would always have a negative slope(but gradually becoming less and less negative). Then it is horizontal (slope = 0) at the minimum. Finally, after crossing the minimum, it has positive slope (and gradually becoming more and more positive). Thus the rate of change of the slope dy/dt, d2y/dt2 is positive at minimum.
2 Integral Calculus
2.1 Indefinite Integral
When we ask ourselves the question which function F(t) will give f(t) =
F(t)
the answer, F(t), is called the indefinite integral of f(t). We also denote,
F(t) =
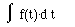
Actually, the answer to that question is not unique, as F(t) + c , where c is a constant , gives the same f(t) on differentiation. So, it is better to write
F(t) =
+ c
Example: Say, as we find for an object in free fall, vy = - g.t we know from differentiation that d( t2 )/dt = 2t . So that d( - 1/2 gt2 ) / dt = - gt
Therefore,
We should put a constant c here, but we could get away with that omission because we have implicitly assumed that y=0 when t=0.
2.2 Definite Integral
If F(t) is the indefinite integral of f(t), then we define the corresponding definite integral as :
f(t)·dt = F(t2) - F(t1)
Here t1 and t2 are called the lower and upper limits of integration.
Example : A car moves from t1 = 2 pm to t2 = 2:10 pm at the constant speed 20 m/s. How far does it go in these 10 min s ?
x(t) =
v(t)·dt = v ·
dt = v· (t2 - t1) = (20 m/s)·(600 s) =12000 m
Example: A brick falls from the top of a 13-story building. 2 s after it has started falling, I see it pass by my eighth floor window. How much further will it fall by the end of 3 seconds of its fall ?
y =
vy ·dt = -
(gt)·dt = - 1/2· g·( t22 - t1 2) = - (4.9 m/s2)·{(32 - 22) s2}
= - 24.5 m
2.3 Definite Integral as an area :
You will find it proved in Calculus texts that the definite integral is actually the area between the f(t) graph and the t-axis, between t= t1 and t= t2 .
Example: A cart, starting from rest, rolls down an inclined plane with uniform acceleration a = -0.49 m/s2 . Draw its v vs t graph. From the graph, find how fast it moves at t =5 s. Also, find graphically the distance it rolls down in 5 s.
Since a = dv/ dt,
v =
a·dt = a·t , as v=0 at t=0
= -(4.9 m/s2)·(5 s) = - 24.5 m/s
To get the distance, one must plot the graph of v vs t, and work out the area between t = 0 and 5 s
x =
v(t)·dt = Area in the v vs t graph
= Area of the triangle = 1/2 ·(5 s)·(4.9 m/s) = 12.25 m