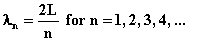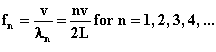Natural Frequencies of Strings

The vibration of a string between two fixed points can be analyzed in terms of its natural frequencies. We will assume that the length of the string is L and that each end of the string is a node, as was the case in the demo that you just saw, and as is the case in the figure shown here.

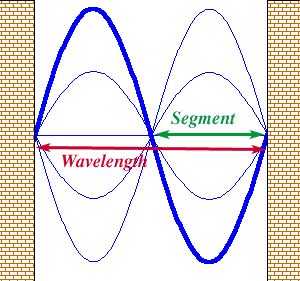
We will define the term segment (see figure) as a closed loop. The length of a segment is thus exactly 1/2 of a wavelength. The number of segments that will fit between the two boundaries is equal to an integer times the number of half-wavelengths

L = 1$\cdot$ ( $\lambda$₁); L = 2$\cdot$( $\lambda$₂); L = 3$\cdot$( $\lambda$₃); ...

In general we can write

L = n ( $\lambda$_n) for n = 1, 2, 3, 4, ...

or

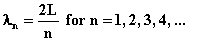
If you play a string instrument, such as a violin or a guitar or even a piano, you are of course much more interested in the natural frequencies. From the velocity equation v = $\lambda$f we obtain for the natural frequencies:

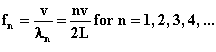
© MultiMedia Physics, 1999/2000